Inventory -- stored resource (raw material, work-in-process, finished goods) that is used to satisfy present or future demand
Inventory management -- determine how much to order? When to order?
ABC Analysis -- classify inventory into 3 groups according to its annual dollar volume/usage
Annual dollar volume = annual demand x cost
An example:
| A | Top 80% of total dollar volume |
| B | Next 15% |
| C | Next 5% |
| Item# | Annual Demand | Cost | Demand x Cost | % of total cost | Class |
| 234 | 50 | 200 | 10000 | 10% | B |
| 170 | 10 | 200 | 2000 | 2% | C |
| 222 | 100 | 800 | 80000 | 80% | A |
| 410 | 50 | 100 | 5000 | 5% | B |
| 160 | 15 | 200 | 3000 | 3% | C |
| Total | 100000 | ||||
Exercise
Pg.541 Problem 13, 27
1. Smooth-out variations in operation performances
2. Avoid stock out or shortage
3. Safeguard against price changes and inflation
4. Take advantage of quantity discounts
1. Holding or carrying costs: storage, insurance, investment,
pilferage, etc.
Annual holding cost = average inventory level x holding cost per unit per year
= order quantity/2 x holding cost per unit per year
2. Setup or ordering costs: cost involved in placing an order
or setting up the equipment to make the product
Annual ordering cost = no. of orders placed in a year x cost per order
= annual demand/order quantity x cost per order
EOQ (Economic Order Quantity) Model
Assumptions
1. Order arrives instantly
2. No stockout
3. Constant rate of demand
What is the order quantity such that the total cost is minimized?
1. Total cost = holding cost + ordering cost
= (order quantity/2) x holding cost per unit per year + (annual demand/order quantity) x cost per order
2. Optimal order quantity (Q*) is found when annual holding
cost = ordering cost
3. Number of orders = Annual Demand/Q*
4. Time between orders = No. of working days per year / number of orders
5. Reorder point = daily demand x lead time + safety stock
Example:
Given:
Annual Demand = 60,000Then, it can be computed:
Ordering cost = $25 per order
Holding cost = $3 per item per year
No. of working days per year = 240
Total cost = $3000
Number of orders = 60000/1000 = 60
Time between orders = 240/60 = 4 days
Daily demand = 60000/240 = 250
If lead time = 3 days (lead time < time between orders)
Reorder point = (60000/240)x3=750
Reorder when inventory on hand = 750
If lead time = 5 days (lead time > time between orders)
Reorder point = 250x5 = 1250
Reorder when inventory on hand = 1250-Q*=1250-1000=250
In class exercise
Pg.540, Problems 10
Annual demand = 2000
Ordering cost = $10
Holding cost = $5
EOQ = sqrt(2*2000*10/5) = 89
Annual ordering cost = 2000/89*$10 = $223.6
Annual holding cost = 89/2*$5 = $223.6
Exercise
Pg. 539, Problem 1, 7a
1. Total cost = holding + ordering + purchasing
2. Holding cost is a % of the purchasing cost
Case 1
Annual Demand =100 per year
Ordering cost = 45 per order
Holding cost = 20% of cost of item
| Order quantity | Cost per item |
| 50 or less | $18 |
| 51 to 59 | $16 |
| 60 or more | $12 |
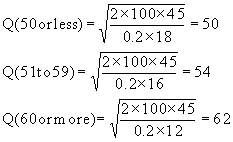
à Should order 62 units
Case 2
Same as case 1 except:
| Order quantity | Cost per item | EOQ | Remark |
| 50 or less | $18 | 50 | |
| 51 to 99 | $16 | 54 | |
| 100 or more | $12 | 62 | Infeasible |
Need to compare:
Total cost (Q=54) and Total cost (Q=100)
Total cost (Q=54) = (100/54)x45 + (54/2)x(0.2x16) + 16x100 =1780.53
Total cost (Q=100) = (100/100)x45 + (100/2)x(0.2x12) + 12x100 = 1425
à Order 100 units
Case 3
Same as case 1 except:
| Order quantity | Cost per item | EOQ | Remark |
| 55 or less | $18 | 50 | Feasible |
| 56 to 99 | $16 | 54 | Infeasible |
| 100 or more | $12 | 62 | Infeasible |
Need to compare:
Total cost (Q=50), Total cost (Q=56) and Total cost (Q=100)
Total cost (Q=50) = (100/50)x45 + (50/2)x(0.2x18) + 18x100 = 1980
Total cost (Q=56) = (100/56)x45 + (56/2)x(0.2x16) + 16x100 =1781.16
Total cost (Q=100) = 1425
à Order 100 units
Pg.540, problem 7b
Exercise
Pg. 540, problems 12, 26