PART I. Multiple Choice
1.
Which
of the following represents valid constraints in linear programming?
a. 2X ≥ 7X × Y
b. 2X × 7Y ≥
500
c. 2X + 7Y ≥
100
d. 2X2 +
7Y ≥ 50
e. All of the above
2.
In sensitivity
analysis, a zero shadow price for a resource means that
a. the resource is scarce
b. the resource constraint was redundant
c. the resource has
not been used up
d. something is wrong
with the problem formulation
e. none of the above
3.
The
feasible region plotted on the diagram below is consistent with which one of
the following constraints?

a. 5x1 - x2 ≤ 0
b. 5x1 - x2 ≥ 0
c. x1 + 5x2 ≤ 0
d. x1 + 5x2 ≥ 0
e. x1 - x2 ≤ 0
4.
The
point of intersection between 2x1 + 7x2 =
10 and -3 x1 + 2x2 = 10 is:
a.
x1 =
1, x2 = 3
b.
x1 =
1, x2 = -3
c.
x1 =
2, x2 = -2
d.
x1 =
2, x2 = 2
e.
x1 =
-2, x2 =2
5.
Which
point is in the feasible solution space defined by the two constraints given
below:
(1) 7x + 3y < 21
(2) x - y < 3
a. x
= 2, y = 1
b. x
= 1, y = -5
c. x
= 8, y = 1
d. x
= 4, y = 4
e. x = 2, y = 8
6.
C&A
company has four stores to be serviced by a
warehouse. The stores’ relative
locations and load information are listed as follows:
|
Stores |
X-Coordinate |
Y-Coordinate |
Load |
|
A |
12 |
15 |
1000 |
|
B |
22 |
9 |
450 |
|
C |
16 |
14 |
750 |
|
D |
14 |
15 |
550 |
Use the
information given and the center of gravity method to determine the coordinates
for the warehouse.
a. x =
13.75, y = 15.13
b. x = 16, y = 13.25
c. x = 13.25, y = 16
d. x = 15.13, y = 13.75
e. x = 4, y = 3.17
Questions 7 and 8.
A product is produced at three plants and shipped to four
warehouses. The transportation costs per
unit, plant capacity, and warehouse demand are given as follows:
|
|
Warehouse 1 |
Warehouse 2 |
Warehouse 3 |
Warehouse 4 |
Capacity |
|
Plant A |
12 |
9 |
13 |
12 |
300 |
|
Plant B |
8 |
14 |
7 |
11 |
300 |
|
Plant C |
14 |
10 |
13 |
10 |
400 |
|
Demand |
200 |
350 |
150 |
300 |
|
7.
C&A
wants to formulate the above problem as a linear program to minimize total
shipping cost. How many decision
variables should be used?
a. 4
b. 6
c. 8
d. 12
e. 15
8.
C&A
wants to formulate the above problem as a linear program to minimize total
shipping cost. How many constraints
should be used?
a. 6
b. 7
c. 8
d. 9
e. 10
9.
Forecasts:
a. become more accurate with longer time
horizons
b. are rarely perfect
c. are more accurate for individual items than
for groups of items
d. all of the above
e. none
of the above
10.
The
primary purpose of the mean absolute deviation (MAD) in forecasting is to:
a. estimate the trend line
b. eliminate forecast errors
c. measure forecast accuracy
d. seasonally adjust the forecast
e. all
of the above
11.
If two
variables were perfectly correlated, the correlation coefficient would equal
to:
a. 0
b. less than 1
c. exactly 1
d. -1 or +1
e. greater than 1
12.
Which one of the following statements about
forecasting is FALSE?
a. You should use the simple moving average
method to estimate the mean demand of a time series that has a pronounced trend
and seasonal influences.
b. The weighted moving average method allows
forecasters to emphasize recent demand over earlier demand. The forecast will be more responsive to
change in the underlying average of the demand series.
c. The most frequently used time series
forecasting method is exponential smoothing because of its simplicity and the
small amount of data needed to support it.
d. In exponential smoothing, higher alpha values
place greater weight on recent demands in computing the average.
e. Casual
methods are used when historical data are available and the relationship
between the factor to be forecast and other external and internal factors can
be identified.
Questions 13
and 14.
C&A Pizza must forecast weekly demand for
special pizzas so that pizza shells can be ordered weekly. Recent demand has
been:
|
Week |
No.
of Special Pizzas |
|
1 |
25 |
|
2 |
23 |
|
3 |
20 |
|
4 |
22 |
|
5 |
23 |
|
6 |
24 |
13.
Using a three-week moving average, what is the
forecast for week 7?
a. 20
b. 21
c. 22
d. 23
e. 24
14.
If a four-week weighted moving average were
used, what would be the forecast for week 7? (The weights are 0.75, 0.25, 0.15,
and 0.10 with the least weight applies to the most recent week.)
a. 21.08
b. 23.24
c. 26.35
d. 27.08
e. 29.05
15.
In setting the control limits to monitor
forecast accuracy through tracking signal, when forecast errors are normally
distributed with a mean of 0, a control limit of three-standard deviation spread from the mean
will be equivalent to:
a.
0 MAD
b.
+/- 1 MAD
c.
+/- 2 MAD
d.
+/- 3 MAD
e.
+/- 4 MAD
16.
A company forecasts the demand for its product
using a trend adjusted exponential smoothing model. The initial forecast is 300 units with a
trend of 50 units. If actual demand was
325 and if alpha = 0.30 and beta = 0.20, then the trend‑adjusted forecast
for the next period would be:
a.
342.5
b.
383.5
c.
391.0
d.
356.0
e.
432.5
Questions 17 and 18.
17.
C&A has the following data on customer
demand for the past 4 weeks:
|
|
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
|
Week 1 |
210 |
178 |
250 |
215 |
160 |
180 |
|
Week 2 |
215 |
180 |
250 |
213 |
165 |
185 |
|
Week 3 |
220 |
176 |
260 |
220 |
175 |
190 |
|
Week 4 |
225 |
178 |
260 |
225 |
176 |
190 |
|
Averages |
217.5 |
178 |
255 |
218.3 |
169 |
186.3 |
What is the seasonal index for
Wednesday?
a.
1.07
b.
1.25
c.
1.93
d.
0.91
e.
0.83
18.
If C&A’s projected demand for week 5 is 1320,
what will be the seasonal adjusted forecast for Wednesday?
a.
275
b.
220
c.
330
d.
412.5
e.
1650
19.
Given the forecast demand and actual demand for
C&A’s product, what is the tracking signal for year 6 if MAD is 12?
|
Year |
Forecast
Demand |
Actual Demand |
|
1 |
78 |
71 |
|
2 |
75 |
80 |
|
3 |
83 |
101 |
|
4 |
84 |
84 |
|
5 |
88 |
60 |
|
6 |
85 |
73 |
a.
+1
b.
-1
c.
+2
d.
-2
e.
cannot be determined
20. The first step managers need to take when making facility location decisions is
a. Begin negotiations with governments for several potential locations
b. Identify specific location possibilities
c. Gather information on location alternatives
d. Evaluate specific sites
e. Identify the location factors that are dominant for the business
PART II. Problem Solving
Question 1.
You
have been assigned a job of recommending the mix of ingredients that go into
the C&A Resin. Your recommendation
has to be based on the following information:
|
Ingredient |
Cost/Pound |
Mixing
Instructions or Requirements |
|
B22 Binder |
$0.30 |
No
more than 4 pounds can be used for each pound of P55 Petroite |
|
T90 Zinc Oxide |
$0.20 |
Maximum
of 60,000 pounds is available per year |
|
P55 Petroite |
$0.40 |
At
least 1 pound must be used for every 4 pounds of B22 Binder |
In
addition, at least 400,000 pounds of C&A Resin will be needed next year.
Formulate
the problem as a linear program to find the least cost mixing recommendation
for C&A Resin.
Question 2.
C&A
Company makes serveral lines of skirts, dresses, and sport coats for
women. Recently it was suggested that
the company should re-evaluate its resources allocation to these products that
would maximize contribution to profits and overhead. Each product must pass through the cutting
and sewing departments. In addition,
each product requires the same fabric.
The following data were collected for the study:
|
Product |
Cutting
(hours) |
Sewing
(hours) |
Materials
(yards) |
|
Skirt |
1 |
1 |
1 |
|
Dress |
3 |
4 |
1 |
|
Sport
Coat |
4 |
6 |
4 |
The
cutting department has 100 hours of capacity.
The sewing department has 180 hours of capacity. 60 yards of materials are available. Each skirt contributes to $5 to profits and
overhead. Each dress $17, and each sport
coat $30.
C&A
uses the following linear program to determine the most profitable product mix:
Let x1
= the amount of skirts to be made
x2 = the amount of dresses to be
made
x3 = the amount of sport coats to be
made
Maximize Z = 5 x1 + 17 x2 + 30 x3
Subjet to:
x1 + 3 x2 +
4 x3 < 100 [Cutting capacity]
x1 + 4 x2 +
6 x3 < 180 [Sewing capacity]
x1 + x2 + 4 x3 < 60 [Materials availability]
x1, x2, x3 > 0
Answer the following questions based on
the given Excel output:
|
Adjustable Cells |
|
|
||
|
|
Cell |
Name |
Original Value |
Final Value |
|
|
$X$1 |
Skirts |
0 |
0 |
|
|
$X$2 |
Dresses |
0 |
20 |
|
|
$X$3 |
Sport Coats |
0 |
10 |
|
Adjustable Cells |
|
|
|
|
|
||
|
|
|
|
Final |
Reduced |
Objective |
Allowable |
Allowable |
|
|
Cell |
Name |
Value |
Cost |
Coefficient |
Increase |
Decrease |
|
|
$X$1 |
Skirts |
0 |
-2.5 |
5 |
2.5 |
1E+30 |
|
|
$X$2 |
Dresses |
20 |
0 |
17 |
5.5 |
9.5 |
|
|
$X$3 |
Sport Coats |
10 |
0 |
30 |
38 |
7.333333333 |
|
|
|
|
|
|
|
|
|
|
Constraints |
|
|
|
|
|
||
|
|
|
|
Final |
Shadow |
Constraint |
Allowable |
Allowable |
|
|
Cell |
Name |
Value |
Price |
R.H. Side |
Increase |
Decrease |
|
|
$B$3 |
Cutting |
100 |
4.75 |
100 |
32 |
40 |
|
|
$B$4 |
Sewing |
140 |
0 |
180 |
1E+30 |
40 |
|
|
$B$5 |
Materials |
60 |
2.75 |
60 |
40 |
26.66666667 |
(a)
What is the optimal product mix?
(b) What is the maximum profit?
(c) What is the effect of an additional yard of
materials on C&A's profit?
(d) How far can you go in reducing the sewing department’s
capacity before this constraint becomes binding?
(e) What is the optimal production mix if the
profit margein of skirts increases by $5?
(f) Someone offers 10 more cutting hours at $1.75
above its standard cost, what would be the maximum acheivable profit?
Question 3.
C&A
wants to use Excel Solver to find a solution to the following transportation
problem. The tables are set up as
follows:
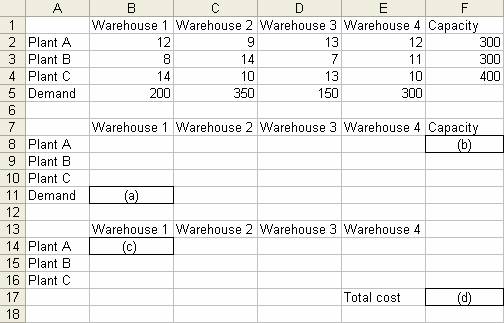
(a)
What should be entered in cell B11 above?
(b)
What should be entered in cell F8 above?
(c)
What should be entered in cell B14 above?
(d)
What should be entered in cell F17 above?
(e)
What should be entered in the “Set Target Cell:”
parameter?
(f)
What should be entered in the “Equal To:”
parameter?
(g)
What should be entered in the “By Changing
Cells:” parameter?
(h)
What should be entered in the “Subject to the
Constraints:” parameter?
Question 4.
Demand for heart transplant surgery at
|
Year |
Time code
(x) |
No. of
surgery (y) |
|
1993 |
-3 |
45 |
|
1994 |
-2 |
50 |
|
1995 |
-1 |
52 |
|
1996 |
0 |
55 |
|
1997 |
1 |
58 |
|
1998 |
2 |
60 |
|
1999 |
3 |
55 |
(a)
C&A decides to use linear regression to predict
the number of surgeries for year 2000.
What is the regression equation for C&A's surgery data?
(b)
What is the number of surgeries for year 2005
using the regression equation in (a)?
(c)
How should you determine whether or not
regression is a good forecasting model for C&A?
(d)
Using exponential smoothing with a=0.2 and a
1998 forecast of 65, find the number of surgeries for year 2000.
(e)
How should you determine whether regression or
exponential smoothing will be a better forecasting model for C&A?