PART I.
Multiple Choice
1. c
2. b
3. a
4. e
5. b
6. d
7. b
8. c
9. d
10. a
PART II. Problem Solving
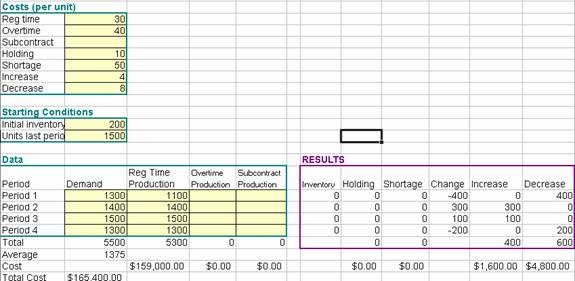
Question 1.
Plan A
Plan B
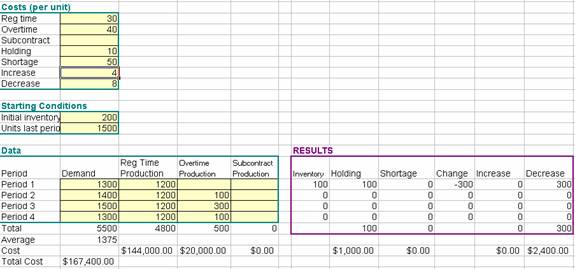
Plan A would cost $165,400,
while Plan B would cost $167,400. In this case it is cheaper to vary work force
than to use overtime (i.e., use Plan A).
Question 2.
a. The EOQ is
194.
b. Total cost
at Q=194 is $774.60
c. The
warehouse will hold only 600/4 = 150 containers.
The annual cost
at Q=150 is 100 x 5 + 75 x 4 = $800.
d.
C&A would
consider paying up to $25.40 ($800-774.60) for a year's rental of enough space
to store 44 additional containers.
e.
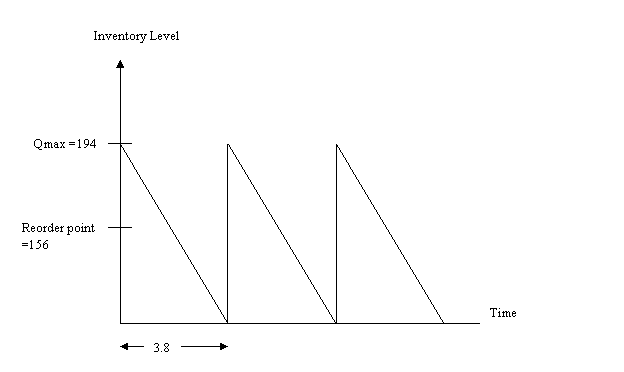
Total number of
orders placed in a year = 15000/194 = 78
Time between orders = 300/78 = 3.8 days
If
lead time is 7 days (> time between orders), reorder point = daily demand x
lead time – EOQ = 15000/300 x 7 – 194 = 156
f.
g.
h. EPQ = 613 units
i. Qmax = EPQ(1-d/p) = 154 units
Length
of production run = 613/20000 x 300 = 10 days
Total
number of production run = 15000/613 = 25
Time
between production run = 300/25 = 12 days
Length
of time with no production = 12-10 = 2 days
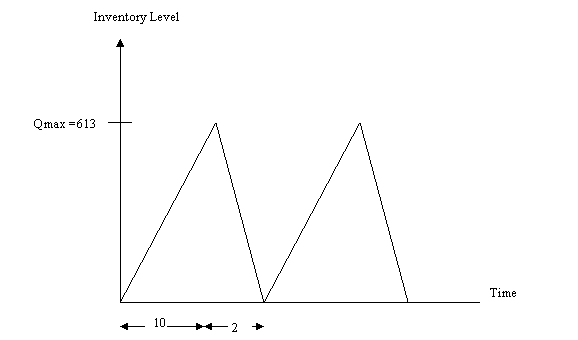
j.
TC(EOQ) = 2 x (15000/194x5)
+ 100x15000 = 1500775
TC(EPQ) = 2 x (15000/613x10) + 80x15000 = 1200490
C&A should produce
k.
EOQ(item cost = $95) = 199
infeasible
TC(EOQ) = 1500775
TC(Q=200) = ordering + holding + item = 375+ 380 + 1425000 =
1425755
C&A
should take the discount
Question 3.
a.
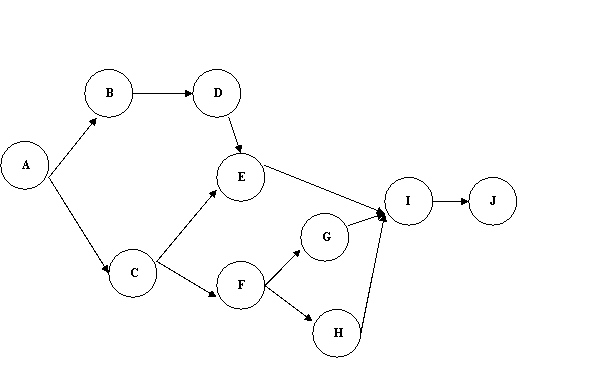
b.
|
Activity |
a |
m |
b |
Expected Time |
ES |
EF |
LS |
LF |
Slack |
Variance |
|
A |
4 |
7 |
10 |
7 |
0 |
7 |
0 |
7 |
0 |
1 |
|
B |
2 |
8 |
20 |
9 |
7 |
16 |
9 |
18 |
2 |
9 |
|
C |
8 |
12 |
16 |
12 |
7 |
19 |
7 |
19 |
0 |
1.777778 |
|
D |
1 |
2 |
3 |
2 |
16 |
18 |
18 |
20 |
2 |
0.111111 |
|
E |
6 |
8 |
22 |
10 |
19 |
29 |
20 |
30 |
1 |
7.111111 |
|
F |
2 |
3 |
4 |
3 |
19 |
22 |
19 |
22 |
0 |
0.111111 |
|
G |
2 |
2 |
2 |
2 |
22 |
24 |
28 |
30 |
6 |
0 |
|
H |
6 |
8 |
10 |
8 |
22 |
30 |
22 |
30 |
0 |
0.444444 |
|
I |
4 |
8 |
12 |
8 |
30 |
38 |
30 |
38 |
0 |
1.777778 |
|
J |
1 |
2 |
3 |
2 |
38 |
40 |
38 |
40 |
0 |
0.111111 |
The critical path is A-C-F-H-I-J
c. LF of J = 40 Weeks
d. 1+1.78+.11+.44+1.78+.11 = 5.22
e.
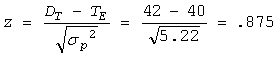
The probability from the standard normal
table is approximately 81%
f. A 95% confidence interval gives a z-value of
1.64
![]() weeks
weeks